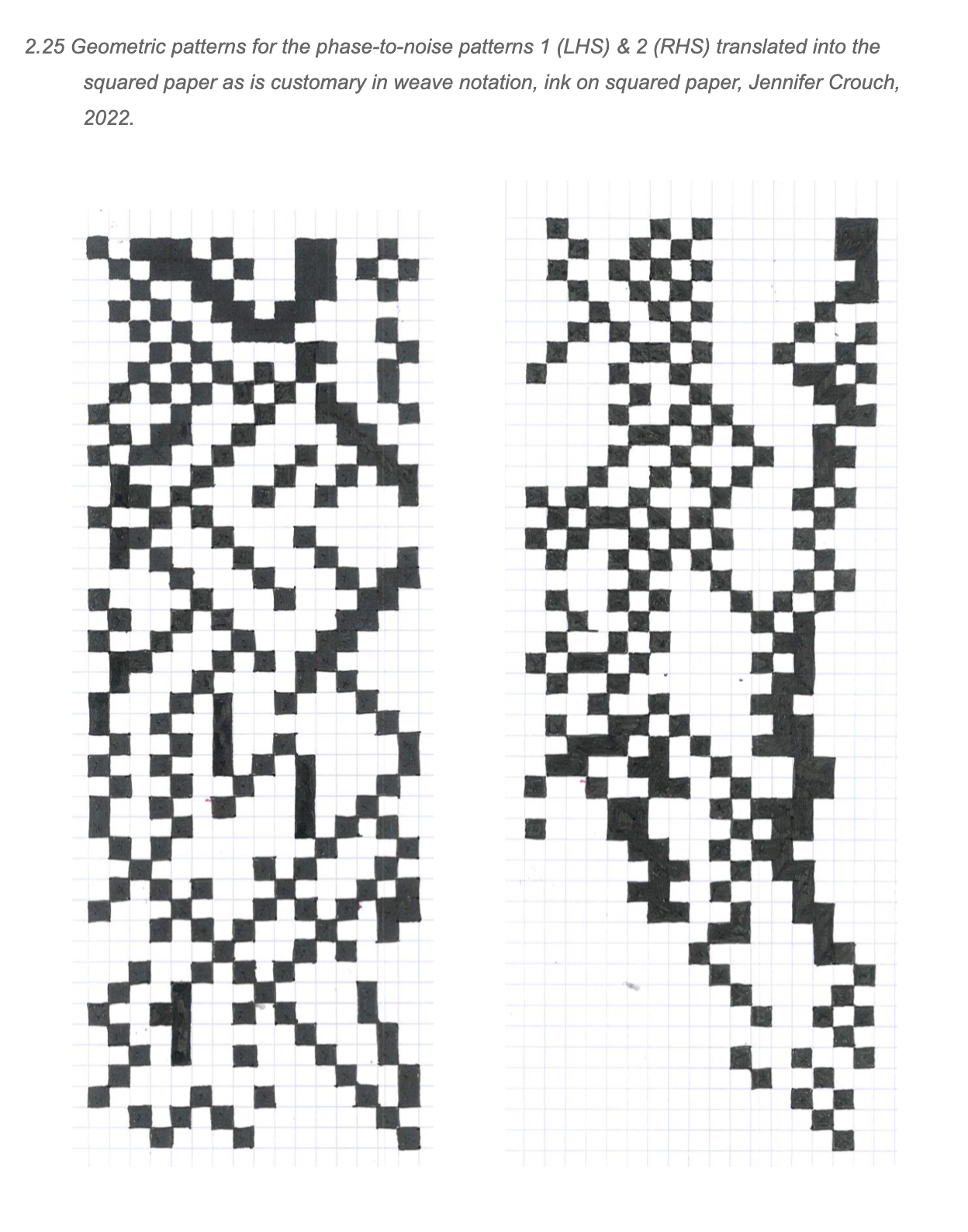Re-corporealising MRI data
The numerical and mechanical relationship between the Dobby loom and the computer is grounded in their shared need for precision and control over warp and weft threads and numerical functions respectively. The computer emerges from the history of weaving. Looms such as the Dobby or Jacquard are said to be “the vanguard of software development” (Hartmann, 2004, p. 53) and as such they form part of the material culture of computation. The mechanical and mathematical relationships between the loom and computation, and the lineage they share is why I choose weaving to explore the analogue-digital interface. Historically, materially and conceptually the loom straddles the analogue and digital. I seek to ‘un-black box’ the computational operations between the analogue NMR signal and the digital MRI image. By combining the mathematical properties of weaving and MRI, this study re-corporealises data abstracted from the body through an embodied craft.



I developed my patterns by looking at the properties of the RF signals and how the FTs, IFTs and k-space transform these geometric, spatial and temporal properties. Cyclicity and symmetries directly feature in the mathematical functions needed in MRI signal analysis and the loom, interestingly this also features in the processes of weaving as the pedal engages the rotating drum in the Dobby engine and this alternatingly lifts and oscilates the movement of the shafts and warp threads. My collaborator at the Francis Crick Institute, Dr Bernard Siow explained that despite the quantum mechanical nature of matter being the reason why NMR exists, ultimately the signal is the most essential aspect of MRI as a technology.
Conceptualising FT and k-space as environments where geometric transformation occurs in space opened up my ability to think of a pattern-making process. The mathematical functions of FT/k-space/IFT act on and transform wave properties such as frequency, phase and amplitude. I decided to develop patterns for these properties. Concurrently, the space where the weft is woven into the warp to create the textile is where the treadling and threading-up interact. This is the interface and environment where textile mattering happens. Siow and I discuss what geometric properties I could create patterns for and how this each property could be represented:
- Frequency: Represented with waveforms either overlapping or separate.
- Amplitude: Represented using rippling/undulating contrasting forms that vary in width and height.
- Phase: Represented using concentric circles as if looking at wood grain to resemble the moiré effect.
- Sequence: Represented with regularly spaced dots and ovals on a connecting line.
- Precession (periodic rotation of the nuclei’s spinning axis): Represented with an elliptical spiral that traces the precessional motion of the spinning nuclei.
- Real and imaginary numbers (R and i): Represented by smooth contrasting forms, some are defined (R) and others merge and are fluid (i)
- Phase-to-noise ratio 1 in ‘the ideal’ situation: Due to the effects of bodily movement, heartbeat and blood flow it is impossible to observe the ‘ideal ratio’ in a living body and only possible in a commercial phantom. This is represented using a curved checkerboard grid to show clearly defined parameters.
- Phase-to-noise ratio 2 in a body: Due to the effects of blood flow, heartbeat, and movement this pattern is represented similarly to number 7 but with merging, dissolving edges contrasting forms. This symbolises that there is always a degree of ambiguity in a scan.
This list of 8 properties and descriptions of how they are drawn covers the spatial-temporal variables required in MRI image processing. I explored these properties by developing a series of initial geometric sketches. As I drew these patterns and translated them into weaving notation I felt as if I was inhabiting and in dialogue with the analogue-digital interface.